ГОРЕ ОТ УМА

или Центральная симметрия

 

 

Мы часто говорим: математика – это красота. Но, увы, это не всегда верно. Очень многое в математике безобразно, скучно и – как это ни странно – довольно глупо, хотя для усвоения этой глупости и требуется, порой, незаурядность ума. Особенно это относится к школьной математике. Чем это можно объяснить? Почему до сих пор математика – один из самых нелюбимых предметов? Если она – действительно красота?

Ниже – рассуждения на эту тему.

 

Треугольник прекрасен, особенно правильный, однако и в нём есть своя дисгармония (математик  спросит, например: почему группа его симметрий не коммутативна?) И вовсе не очевидно, что треугольник общего вида – самое наглядное, что только может быть в геометрии. Почему же школа так их любит? Объяснение просто: существует множество (десятки тысяч) задач про треугольники. Их придумали потому, что треугольники в течение уже более полутора веков служили кормушкой многочисленным репетиторам и замечательным средством отсеивать абитуриентов при приёмке в вузы. С точки же зрения большой математики треугольник не есть фундамент ни для чего (во всяком случае, в тех аспектах, которые изучаются в школе). Гораздо более фундаментальны – преобразования симметрии (зеркальной, центральной и орнаментальной).

Вывод теорем программы для 7 и 8 класса на основе центральной симметрии очень короток и элементарен. Тем не менее, после «понтрягинской контрреволюции» нет ни одного учебника, поступающего так. Поэтому - вот своего рода «меморандум» такого подхода: чтобы мы хотя бы не забыли, что он существует.

Центральная симметрия. Накладываем на плоскость кальку, перечерчиваем фигуру, вкалываем иголку в некую точку, называемую центром симметрии, поворачиваем на 180^о (можно и по часовой, и против). Фигура на кальке перемещается. Если О – центр симметрии, то луч ОА переходит в дополнительный луч ОА₁, а точка А – в точку А₁, причём |ОА|=|ОА₁|. Центральная симметрия – вид движения, так как сохраняет расстояния: |f(A),f(B)|=|A,B| (здесь прямые скобки обозначают расстояние, f – центральная симметрия).

Если при центральной симметрии фигура переходит в себя, то она называется центрально-симметричной (или имеющей центр симметрии). Примеры центрально-симметричных фигур буквально «пронизывают» курс математики в средней школе: 1) график линейной зависимости y=ax, 2) график y=xⁿ, где n – нечётно, 3) график синуса, 4) гипербола у=1/х, 5) буква S, 6) двойная спираль, 7) параллелограмм и так далее. Чувствуется, что центральная симметрия – более утончённый вид симметрии, нежели, скажем, зеркальная.

Докажем несколько простых свойств.

1.     При центральной симметрии не существует неподвижных точек, кроме центра симметрии. И действительно: каждая точка, кроме центра, переходит в точку дополнительного луча.

2.     Если при центральной симметрии фигура F переходит в фигуру F₁, то фигура F₁ переходит в фигуру F. Очевидно, если точка А переходит в А₁, то и А₁ переходит в А. И так – любая точка фигур F и F₁.

3.     Вертикальные углы равны. Очевидно, так как они центрально симметричны относительно их общей вершины.

4.     При центральной симметрии прямая, не проходящая через центр симметрии, переходит в параллельную себе прямую. (Если же прямая проходит через центр симметрии, то она переходит в себя, но это очевидно).

                                                          

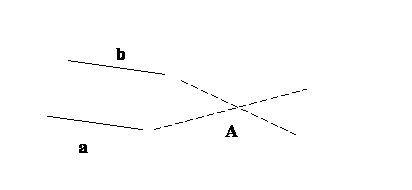
Пусть прямые а и b пересекаются в т. А. Тогда АÎа Þ f(A)Îb, АÎb Þ f(A)Îa,  f(A)ÎaÇbÞf(A)=A. Но этого не может быть, так как АÎа и, следовательно, не является центром симметрии.

         Отсюда вытекает теорема о равенстве внутрених накрест лежащих углов: они симметричны относительно центра отрезка, отсекаемого параллельными от секущей. Из равенства внутренних накрест лежащих углов следует, что сумма внутренних углов треугольника 180^о…

Тот, кто впервые встречается с методом преобразований, переживает просто шок, настолько всё быстро доказывается. Действительно, так и должно быть – ведь группы преобразований куда фундаментальнее, чем структуры конгруэнтности углов и отрезков (это стало ясно уже после Эрлангенской программы Клейна). Однако в последнее время преобразования явно вышли из школьной моды. Не потому, что они плохи, наоборот, они просто СЛИШКОМ ХОРОШИ, и поэтому с ними не получается сложных экзаменационных задач. И мы просто вынуждены учить людей быть умными  дураками. Поистине: горе от ума.

Я не призываю к новой “революции”: уже она была, и стало ясно, что начинать нужно было с другого конца. Хочу лишь ещё раз напомнить о существовании гораздо более эффективных методов доказательства всех школьных теорем и решения всех школьных задач, чем тот, которому мы учим. Потому что либо наше образование будет двигаться вперёд, и тогда неизбежно придёт день, когда мы перестанем учить по-старинке, либо все наши сегодняшние размышления могут быть любыми, хуже от этого не станет (но и лучше – тоже).

 

ДОБАВЛЕНИЕ 2007 ГОДА.

Метод преобразований – в основе известного учебника А.Н.Колмогорова по геометрии – тут не нужно ничего изобретать. Однако «колмогоровская революция» семидесятых годов закончилась в тот момент, когда школьники, проучившиеся по новым учебникам школьный курс стали поступать в вузы. Оказалось: стандартную абитуриентскую геометрию они знают гораздо хуже. Но ведь это так и должно было быть. Ребята учили то, чему их учили. А спрашивали с них по-старинке. Главный недостаток колмогоровской реформы состоял, как видно, в том, что тот же самый старый материал, старое содержание просто попытались налить в новые мехи. Соответственно, одно к другому не подошло. Тогда как резкое сокращение традиционного материала (по части доказательств), которого удается добиться, ПОЗВОЛИЛО БЫ ВКЛЮЧИТЬ БОЛЬШОЙ НОВЫЙ МАТЕРИАЛ, доведя программу до математики 20-го века.

«Старая» (одна же – действующая) программа – это просто тест для отсеивания тех, кто не имеет математических способностей. Часть ребят его выдерживает и попадает в вуз, где продолжает обучение математике. Другая часть детей – не выдерживает, и остается на уровне математики 17 века. Эта часть математики имеет не очень большое практическое и культурное значение. Попытка создать еще информатику – параллельно традиционной математике – неудачна, т.к. между обычной математикой и информатикой сохраняется неустранимая идейная дистанция… Для практических целей не нужны уже обыкновенные дроби, не случайно их нет на простом калькуляторе. Обыкновенные дроби включены в программу как пропедевтика радиональных дробей в алгебре! В «жизни» они совершенно никому не нужны. А это – 4-й и 5-й классы. Поэтому реальный школьник выходит за ворота школы с подробным знанием многих совершенно ненужных вещей и без малейшего представления о том, что происходит в реальной науке под названием «математика».

Я очень много писал обо всем этом. Но, Маяковский правильно заметил, что «голос единицы тоньше писка».